
撰文 | 夏志宏
● ● ●
公元1610年,天文学家伽利略发现了太阳黑子,这在欧洲引起了极度恐慌。从亚里士多德以来,人们一直认为太阳是完美无缺的。太阳黑子的存在破坏了这些根深蒂固的文化理念。太阳有缺陷这个事实也与当时的宗教教义所相悖。
同样,人们一直认为数字是完美无缺的,无理数的发现使一群数学迷们异常惊恐。为了防止世人窥视到上帝的缺陷,发现者被绑上石头,沉入海底。
公元前第五世纪,古希腊毕达哥拉斯(pythagoras)学派倒霉的希勃索斯(hippasus)发现了一个惊人事实,一个边长为一的正方形的对角线长度不是有理数。无理数的存在说明了数轴上存在不能用有理数表示的“空隙”,和毕达哥拉斯学派的“万物皆为数(有理数)”的哲理大相径庭。学派领袖惶恐、愤怒以后,可怜的希勃索斯被百般折磨,判了极刑。从此毕达哥拉斯学派把守住这一秘密当成学派的头等大事。
在人类科学史上,以“主义”、“思想”等教条来“指导”、“武装”科学研究时,其结果往往是悲剧。
根据勾股定理(在西方叫毕达哥拉斯定理),边长为一的正方形的对角线长度为
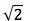
,也就是说,希勃索斯是第一个发现
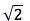
是无理数的人。
根据古希腊哲学家柏拉图《对话录》记载,数学家theodorus of cyrene发现了从2到17整数中,除了4,9,16这几个完全平方数而外,所有的平方根都是无理数。柏拉图没有解释theodorus为何停在17。事实上,可以证明任何正整数的平方根如果不是恰好是整数的话,那一定是无理数。
无理数的发现经常被称为数学史上的第一次危机,其影响是深远的。有理与无理的对立不仅有抽象的哲学意义,也有广泛的应用意义。
两个实数的比例如果是有理数,我们称这两个实数有理相关。在力学上,震动频率的有理相关会引起共振,而共振会带来系统的不稳定。举个小例子,如果人在木桥上走动的频率与木桥晃动的固有频率有理相关,就会引起危险的共振现象。
再举个例子,太阳系在火星和木星之间有众多的小行星,形成一个小行星带。已发现并确认的就有几十万颗。这些小行星在太空中的分布和它们的轨道稳定性有密切关系。如果小行星绕太阳的运动周期和木星的周期比例是有理数,这就形成共振,它们之间的相互影响就会很大,这些影响往往会导致小行星轨道的不稳定。因此,在这些轨道上小行星的数目就会很少。小行星分布的著名kirkwood空隙就是在这些共振区域。比较大的空隙是3:1、5:2、7:3和2:1等共振区域。
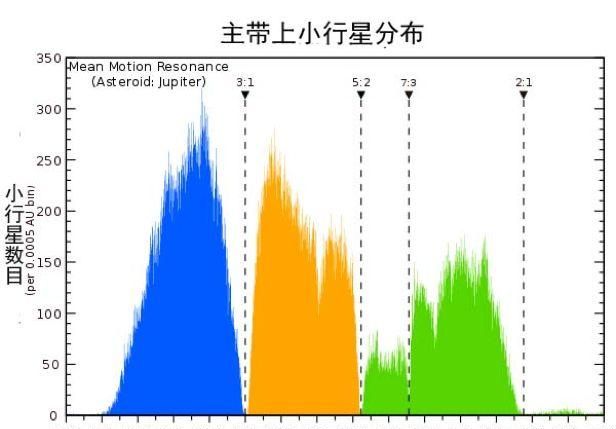
在音乐上,频率共振会带来和谐和美感,但无理数的出现却带来了一些尴尬及无奈。基音——比如c音,频率为261hz——确定以后,高八度就是c的频率的两倍522hz。从c到高音c之间,如何确定其它音阶的频率是一个非常有趣的问题。
两个共振频率放在一起会令人听起来爽心悦耳,3/2是仅次于2/1共振的最为简单和纯粹的共振。按照毕达哥拉斯创建的“五度相生律”,如果基音是c,纯五度则定为c频的3/2倍;纯四度定为c频降3/2后再乘以2,也就是c的4/3;纯二度定为3/2平方除以2;纯六度为3/2的立方除以2。八度的其它音级的频率都是以类似的五度相生而产生。
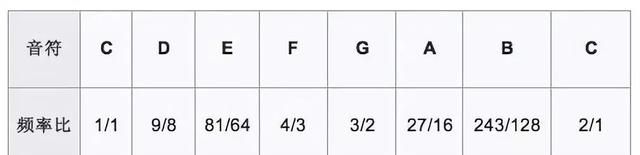
由“五度相生律”所产生的八度可分为十二个音程,音程之间距离并不相等。现代音乐为了便于基音的改变和转调,不得不把八度平均分成十二个半音音程,使得各相邻两音之间的频率之比完全相等,如此得到的即是所谓的“十二平均律”。十二平均律基音改变以后音阶的比例也会完全一致。十二平均律在交响乐队和键盘乐器中得到广泛使用,现在的钢琴即是根据十二平均律来定音的。
但非常遗憾的是,十二平均律半音的频率比为2的1/12次方,是一个无理数。而且每两个音的频率比,除了高八度外,都是无理数。比如,纯五度音程的两个音的频率比为2 的7/12 次方,是个无理数,大约等于1.4983,和自然泛音序列的1.5有些差别。同样,其它和弦音符都跟“五度相生律”序列中的几个音符不一样。所幸的是,纯五度、纯四度、大三度等在十二平均律中和3/2,4/3,5/4非常接近,常人听不出什么区别。正因为如此,小号等靠自然泛音序列定音的按键吹奏乐器得以在交响乐队演奏,而没有明显的违和感。
最后,关于无理数的性质有很多有趣的数学问题。比如,黄金分割是所有无理数中最“无理”的无理数。有意思的是,无理数不仅存在,而且事实上比有理数多得多。
——2018.7. 深圳
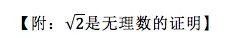
我们用反证法。假定
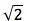
是有理数,也就是说
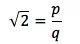
这里p和q都是正整数,我们可以假定p和q互为素数,也就是说p和q没有公因子。等式两边平方以后,得到
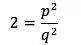
也就是说
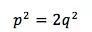
因此p必须是偶数,也就是说p=2k,k为一正整数。我们因此得到
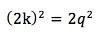
或者
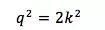
因此,q也必须是偶数。p和q都是偶数,与p和q互素的假定矛盾。
证毕。


公众号、报刊等转载请联系授权
凯发k8官网 copyright@zhishifenzi.com
商务合作请联系
business@zhishifenzi.com
知识分子为更好的智趣生活 id:the-intellectual
本网页内容旨在传播知识,若有侵权等问题请及时与本网联系,我们将在第一时间删除处理。e-mail:dandanxi6@qq.com